Introduction

Battleship is two player guessing game played on a grid. Players secretly place non overlapping ships on their own grid horizontally or vertically. Each ship takes up a certain amount on the grid and the goal is to sink all the enemy ships by taking turns guessing at the locations. If a ship is hit, it is reported and if it is sunk by guessing all points the ship is on it is reported.

Games will be simulated using two different methods, traditional and using a density grid. The traditional method involves randomly guessing at locations and if a hit occurs, the area around it is searched until the ship is sunk. The density grid method uses the remaining ships and knowledge of missed shots to create a density grid of likely places the ships may be. The two methods will be shown and average guesses it takes to win.

Game Setup

To create the game, a grid will be used and populated with five ships. The ships will have a size of 5, 4, 3, 3, and 2 placed randomly on the grid either vertically or horizontally and no overlaps.

Ships

The ships will be stored as a data frame:

ships <- data.frame(name=c("Carrier", "Battleship", "Submarine", "Cruiser", "Patrol"),
                    size=c(5,4,3,3,2), id=1:5)

Grid

The grid will be a 10x10 matrix of zeros.

ncol <- 10
nrow <- 10
buildGrid <- function(ncol, nrow) {
  return(matrix(0, ncol=ncol, nrow=nrow))
}

grid <- buildGrid(ncol, nrow)

The next step is to populate the grid with the ships. The ships will be looped over and checked if overlaps or out of bounds and if not, place it.

popGrid <- function(grid, ship.sizes, ship.id) {
  ## Very basic 
  # Make sure grid is blank
  if (any(grid != 0)) {
    stop("Grid has some information already on it")
  }
  # Check if ship.sizes is valid
  if (is.null(ship.sizes) | any(is.na(ship.sizes))) {
    stop("Ship sizes is null or NA")
  }
  # Make sure ship.sizes are <= grid size... probably should check if everything can fit
  if (any(ship.sizes > ncol(grid)) && any(ship.sizes > nrow(grid))) {
    stop("Grid size is smaller than ship sizes")
  }
  
  # Tolerance for check
  tol <- .Machine$double.eps ^ 0.5
  
  # Loop over ship sizes and fill in
  for (k in 1:length(ship.sizes)) {  
    # Check if ship placed
    isPlaced <- FALSE
    # If outside bounds or occupied get new
    while(!isPlaced) {
      # Generate a random direction
      hv <- sample.int(2, size=1)
      # place ship
      row <- sample.int(nrow(grid), size=1)
      col <- sample.int(ncol(grid), size=1)
      ## Since know the direction, checking becomes easier
      # Horizontal
      if (hv == 1) {
        # Check if fits in grid boundaries and not occupied
        if (col+ship.sizes[k] < ncol(grid) && all(grid[row, col:(col+ship.sizes[k]-1)] == 0)) {
          grid[row, col:(col+ship.sizes[k]-1)] <- ship.id[k]
          isPlaced <- T
        }
      }
      # verticle
      if (hv == 2) {
        # Check if fits in grid boundaries and not occupied
        if (row+ship.sizes[k] < nrow(grid) && all(grid[row:(row+ship.sizes[k]-1), col] == 0)) {
          grid[row:(row+ship.sizes[k]-1), col] <- ship.id[k]
          isPlaced <- T
        }
      }
    }
  }
  return(grid)
}

board <<- popGrid(grid, ships$size, ships$id)

Traditional

The traditional method of playing is to guess a location and if it is a hit, search around area until ship is sunk. This is repeated until all ships are sunk.

Create random guesses

genGuesses <- function(nrow, ncol) {
  # Generate all possible combinations
  r.ran <- rep(1:nrow, nrow)
  c.ran <- rep(1:ncol, each=ncol)
  # Put it into a data frame and shuffle it
  df.ran <- data.frame(r=r.ran, c=c.ran)
  df.ran <- df.ran[order(sample(nrow(df.ran))),]
  return(df.ran)
}

Guess and Search

The idea here is to continue guessing and searching until there are no more ships left. A guess will be marked with a -1 and ships are marked with values greater than 0, when there is no more values in the grid greater than zero, the ships are all hit and the game is over.

To search would be best done with stack, pushing a hit onto it, pop it off and search around it and add any new hits onto it. This will be mimic’d in R using a recursive function.

# Recursive function to search area, board is set to parent scope 'global' and <<- is used to set values
recSearch <- function(row, col) {
  # If value <= 0 then its searched or open water
  if (board[row,col] <= 0) {
    # Set position on board
    board[row, col] <<- -1 # Set value to 'global'
    return(board)
  } else {
    board[row,col] <<- -1 # Set value to 'global'
    # Search left, right, up, down for ships
    if (row+1 <= nrow(board)) {
      recSearch(row+1, col)
    } 
    if (row-1 > 0) {
      recSearch(row-1, col)
    } 
    if (col+1 <= ncol(board)) {
      recSearch(row, col+1)
    } 
    if (col-1 > 0) {
      recSearch(row, col-1)
    }
  }
}

Now can combine the search function with guessing, the generated board will be set as a semi global variable using the «- operator.

# Guesses will be marked as a -1, continue guessing until no more positive values >0
guessSearch <- function(ncol, nrow, ships) {
  ship.sizes <- ships$size
  board <<- popGrid(buildGrid(ncol, nrow), ship.sizes, ships$id) # Set to global
  df.ran <- genGuesses(nrow,ncol)
  idx <- 1 # counter to go through df.ran
  while(any(board > 0) && idx <= nrow(df.ran)) {
    b.value <- board[df.ran$r[idx], df.ran$c[idx]] # board value
    if (b.value > 0) {
      recSearch(df.ran$r[idx], df.ran$c[idx])
    } else if (b.value == 0) {
      board[df.ran$r[idx], df.ran$c[idx]] <<- -1
    }
    idx <- idx + 1
  }
  return(sum(board == -1)) # Return number of guesses
}

Simulate a million games and record the number of guesses taken:

n <- 1000000
gs <- as.numeric(n)

for (k in 1:n) {
  gs[k] <- guessSearch(10,10, ships)
}

Density Method

The idea of this is to build up a density of where the ships can be and guessing at the highest density places first. When a ship is found, the area around it like before.

Creating Density of Ships

To create this, all possible places where the ships can be located is built up in a matrix. This is done by looping over the grid and checking if there was a miss. This will serve as the density grid.

buildDen <- function(nrow, ncol, ship.sizes) {
  den <- buildGrid(ncol, nrow) # create base grid
  # Loop over ships
  for (k in 1:length(ship.sizes)) {
    # Build density by looping over
    for (j in 1:(nrow-ship.sizes[k]+1)) {
      for (i in 1:ncol) {
        if (!any(board[j:(j+ship.sizes[k]-1),i] == -1)) {
          den[j:(j+ship.sizes[k]-1),i] <- den[j:(j+ship.sizes[k]-1),i] + 1
        }
      }
    }
    # Now columns
    for (j in 1:nrow) {
      for (i in 1:(ncol-ship.sizes[k]+1)) {
        if (!any(board[j,i:(i+ship.sizes[k]-1)] == -1)) {
          den[j,i:i:(i+ship.sizes[k]-1)] <- den[j,i:i:(i+ship.sizes[k]-1)] + 1
        }
      }
    }
  }
  return(den)
}

Ship Ids

We need to update ship ids for the density grid so when ships are destroyed the density grid is properly recreated.

updateShips <- function(ships) {
  # Need to update ship ids
    ids <- unique(c(board))
    ids <- ids[ids > 0]
    ships <- ships[ids %in% ships$id,]
    return(ships)
}

Density Search

Set up density search, this is almost identical to the Guess Search earlier just now creates a density grid to search with:

denSearch <- function(ncol, nrow, ships) {
  ship.sizes <- ships$size
  board <<- popGrid(buildGrid(ncol, nrow), ship.sizes, ships$id) # Set to global
  den <<- buildDen(nrow,ncol, ship.sizes)
  # Since ship sizes
  while(any(board > 0)) {
    ships <- updateShips(ships)
    # Get highest board value
    idx <- which(den == max(den), arr.ind = TRUE)
    b.value <- board[idx[1,1], idx[1,2]] # board value
    if (b.value > 0) {
      recSearch(idx[1,1], idx[1,2])
    } else if (b.value == 0) {
      board[idx[1,1], idx[1,2]] <<- -1
    }
    den <<- buildDen(nrow,ncol, ship.sizes)
  }
  return(sum(board == -1)) # Return number of guesses
}

Set up simulation:

n <- 1000000
ds <- as.numeric(n)

for (k in 1:n) {
  ds[k] <- denSearch(10,10, ships)
}

Results

res.df <- data.frame(Average=c(round(mean(gs),2), round(mean(ds),2)), Standard.Deviation=c(round(sd(gs),2), round(sd(ds),2)))
row.names(res.df) <- c("Random Guess", "Density Grid")
kable(res.df, align='c')

	Average	Standard.Deviation
Random Guess	67.25	12.33
Density Grid	57.91	7.75

Looking at the histograms:

df <- data.frame(vals=c(gs,ds), id=c(rep("Guess", n), rep("Density", n)))
ggplot(df, aes(x=vals, colour=id)) + geom_density(size=1.5) + 
  xlab("Turns") + ylab("")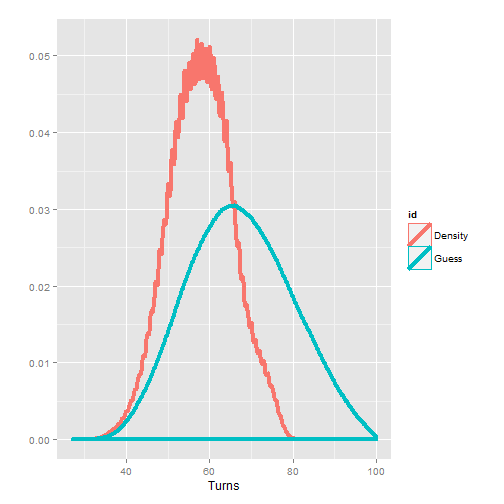

As expected, randomly guessing at ship locations can be greatly improved with a little math. Not only did it take about 10 fewer turns, the variance has been reduced.

Extra

The one section that can be greatly improved is searching around a ship once it is found. The way this was implemented was a very naive way of doing it. In reality, all the points are never guessed and once the way a ship is facing, the guesses are directed in that direction. This could be implemented and should reduce both methods number of turns. As well, the implementation in R is really bad and should of been done in another language for efficiency.